We point a sensor at the night sky expecting to see a satellite. It is not there. As the absence of evidence is not the
evidence of absence, we have to make use of this information to the maximal extend allowed, but how? My new approach
reformulates Bayesian inference as a geometric problem of uniform distributions on convex H-polytopes and H-polyhedra.
In this formulation Bayesian inference simply becomes matrix and vector concatenation. Extending this idea to mixture
models of uniform distributions on H-polytopes allows us to create methods that converge to true Bayesian inference in
distribution. This allows us to ``subtract out'' the sensor window from our measurement of uncertainty about where the
satellite with little additional computational cost.
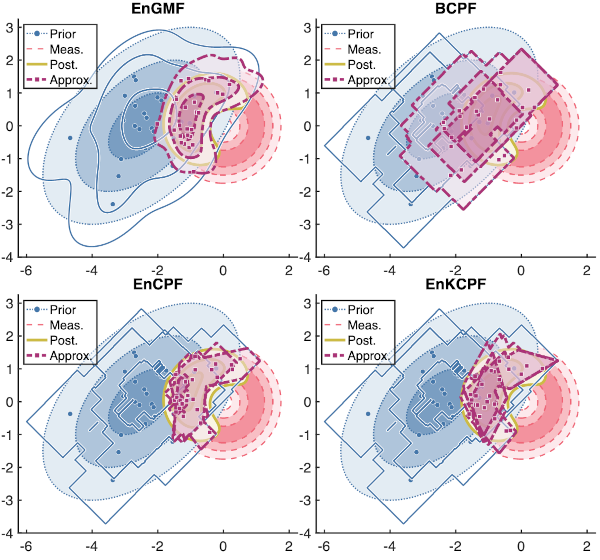
In the figure above, the top left panel is the action of the ensemble Gaussian mixture filter (EnGMF) on the banana problem
which is a common problem in aerospace settings. The top right panel is a naive version of a bootstrap polytope filter,
meaning that the filter simply assumes naive updates of our uncertainty from prior to posterior. The bottom left figure
is a theoretical polytope filter that generalizes the convex polytope filter to polytope mixture models. The bottom right
panel is a generalization of Kalman filter updates for polytopes and polytope mixtures, and is probably the most promising
geometric filter at the moment.
In the figure above a state (blue line) is evolved through a simple ordinary differential equation tracing the path along a
circle. A measure of our uncertainty about this state is evolved through a corresponding polytope tangent linear model (PTLM)
represented by the purple square.