I am a computational scientist; I create methods that enable practitioners to make better predictions and make smarter
decisions while using as little computational power as is practical. My primary research focus is on Bayesian inference
and uncertainty quantification in the broad sense, with a particular focus on computational methods for uncertainty
quantification in medium-to-large scale scientific problems such as multi-target tracking, sensor tasking, data
assimilation, and equation discovery.
How can we make use of computer models that are untrustworthy, like those created by data-driven methods such as neural
networks? Multifidelity and model forest methods build a hierarchy of models where the principal, top-level, model is
based on theory and expert understanding, meaning that it is trustworthy. The subsequent lower level models are all less
trustworthy than the principal model, meaning that these so-called ancillary models can for-go theory and instead be based
on data. Models such as neural-networks, and reduced-order models can be very cheap for the predictive power that they
provide, but are much less interpretable and much less trustworthy.
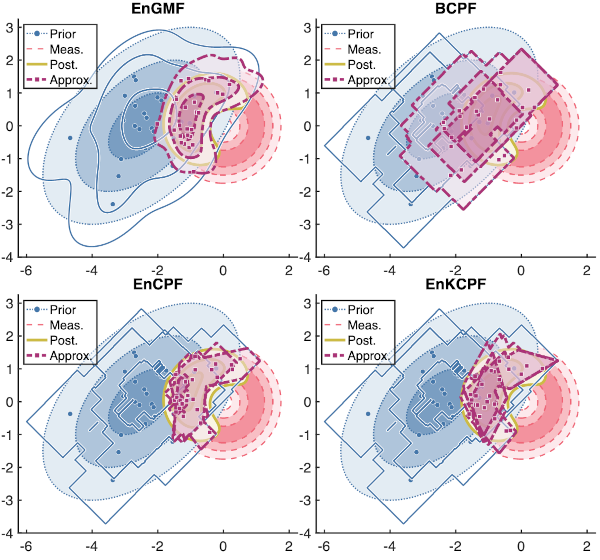
We point a sensor at the night sky expecting to see a satellite. It is not there. As the absence of evidence is not the
evidence of absence, we have to make use of this information to the maximal extend allowed, but how? My new approach
reformulates Bayesian inference as a geometric problem of uniform distributions on convex H-polytopes and H-polyhedra.
In this formulation Bayesian inference simply becomes matrix and vector concatenation. Extending this idea to mixture
models of uniform distributions on H-polytopes allows us to create methods that converge to true Bayesian inference in
distribution. This allows us to ``subtract out'' the sensor window from our measurement of uncertainty about where the
satellite with little additional computational cost.
Traditional particle filter resampling is driven only by some approximation of our posterior uncertainty. This ignores
any prior knowledge that we have about the dynamics. In this project we aim to build normalizing flows that act as
discriminators for the resampling step of a particle filter. The resampling that we propose will reduce the dimension of
the resampling step from the dimension of Euclidean representation to that of the dimension of the underlying manifold
of the dynamics.